Entropie informațională
În teoria informației, entropia Shannon sau entropia informațională măsoară incertitudinea asociată cu o variabilă aleatoare. Această măsură indică și cantitatea de informație conținută într-un mesaj, exprimată de obicei în biți
sau în biți pe simbol. Când este exprimată în biți, ea reprezintă
lungimea minimă pe care trebuie să o aibă un mesaj pentru a comunica
informația.
Ea mai reprezintă și o limită absolută a celei mai bune compresii
fără pierderi aplicabilă unor date comunicate: tratând un mesaj ca pe o
serie de simboluri, cea mai scurtă reprezentare posibilă a mesajului
are lungimea egală cu entropia Shannon în biți pe simbol înmulțită cu
numărul de simboluri din mesajul original.
O aruncare a monezii are entropia de un bit. Dar, dacă moneda nu este
echilibrată, atunci incertitudinea este mai mică (se știe că există o
probabilitate mai mare ca ea să cadă cu o anume parte a ei în sus), și
astfel entropia Shannon este mai mică. Un șir lung de caractere repetate
au entropia 0, deoarece fiecare caracter este previzibil. Entropia unui
text în limba engleză este de 1,0 până la 1,5 biți pe literă,
. Echivalent, entropia Shannon măsoară media de conținut informațional
pe care receptorul o pierde atunci când nu cunoaște valoarea variabilei
aleatoare.
Conceptul a fost introdus de Claude Shannon în lucrarea sa din 1948 „O teorie matematică a comunicației”.
Definiție
Entropia H a unei variabile discrete X cu valorile {x1, ..., xn} și funcția de probabilitate p :
iar dacă X este continuă, având funcția de distribuție f(x):
unde b este o bază pentru logaritmi, reală și supraunitară (de obicei
2, caz în care unitatea de măsură a informației se numește bit, sau e, caz în care ea se numește nat).
Exemplu
Presupunem evenimentul aruncării unui zar cu 6 fețe. Valorile variabilei X sunt {1,2,3,4,5,6} iar probabilitățile obținerii oricărei valori sunt egale. Entropia este:  .
.
 .
.
Pentru o populație discretă cu valorile {1,2,3,4,5,6} cu probabilitățile respectiv {3%,16%,31%,31%,16%,3%} (aproximativ o distribuție binomială cu p=50%) entropia calculată este:  . Incertitudinea s-a diminuat față de exemplul precendent.
. Incertitudinea s-a diminuat față de exemplul precendent.
 . Incertitudinea s-a diminuat față de exemplul precendent.
. Incertitudinea s-a diminuat față de exemplul precendent.Proprietăți
Aditivitate
Logaritmul este folosit în calculul entropiei pentru a pemite adunarea incertitudinii unor variabile independente.
De exemplu, considerând X și Y doua evenimente independente, distribuite uniform, cu  respectiv
respectiv  posibile rezultate perechea (X,Y) va avea
posibile rezultate perechea (X,Y) va avea  rezultate echiprobabile
rezultate echiprobabile 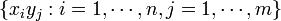 . Entropia perechii (X,Y) se calculează:
. Entropia perechii (X,Y) se calculează:
 respectiv
respectiv  posibile rezultate perechea (X,Y) va avea
posibile rezultate perechea (X,Y) va avea  rezultate echiprobabile
rezultate echiprobabile 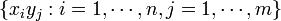 . Entropia perechii (X,Y) se calculează:
. Entropia perechii (X,Y) se calculează:
Astfel, entropia perechii este egală cu suma entropiei celor două
evenimente luate separat. Proprietatea aditivității implică faptul că
entropia se menține constantă indiferent dacă mulțimea
rezultatelor/procesul este privit ca întreg sau ca sumă a unor
submulțimi / procese.
Schimbarea de bază
Entropia poate fi calculată folosind diferite baze ale logaritmului. Înmulțirea logaritmilor are proprietatea:  .
.
 .
.
Entropia calculată in baza  va fi egală cu
va fi egală cu  inmulțită cu entropia calculată cu logaritm in baza 2.
inmulțită cu entropia calculată cu logaritm in baza 2.
 va fi egală cu
va fi egală cu  inmulțită cu entropia calculată cu logaritm in baza 2.
inmulțită cu entropia calculată cu logaritm in baza 2.Continuitate
Entropia este o funcție continuă. Unei modificari infinitezimale a
probabilităților corespunde o modificare asemănătoare a entropiei.
Simetrie
Valoarea entropiei rămâne neschimbată daca se schimbă ordinea variabilelor xi.
 etc.
etc.
Maximum
Entropia, incertitudinea atinge o valoare maximă dacă evenimentele sunt echiprobabile.
Pentru evenimente independente și echiprobabile entropia crește cu numărul posibil de rezultate.
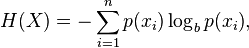




Niciun comentariu:
Trimiteți un comentariu